Balanced Catan Board Generator
last updated 2022-06-29 11:22:04 by Simon Vandevelde
Catan is a wonderful boardgame about strategy and chance.
However, the chances of the game can become extremely skewed based on the board layout, which is typically decided randomly.
This post describes how we can tackle this, and implements a tool (available online) to generate balanced boards using the IDP-Z3 reasoning engine, based on First Order Logic.
Image from the Wikimedia Commons.
Catan boards and balance
Lets first get into what constitutes a Catan board.
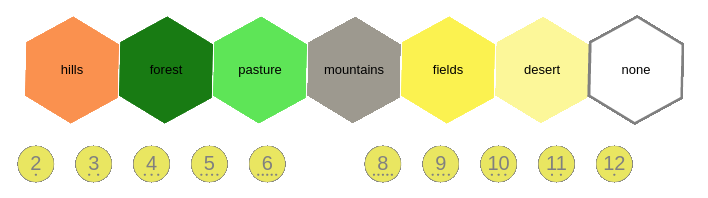
As shown in the image above, a Catan board consists of a hexagonal grid containing 19 hexes.
Each hex is represented by a resource tile: the forest (wood), pasture (wool) and fields (grain) resources appear four times, while hills (stone) and mountains (ore) appear three times.
Finally, there is a single desert tile which is barren and therefore without resources.
Each hex is also assigned a token containing a number: when this number is rolled with the dice, the accompanying resource is paid out to the players with neighbouring settlements.
There are two tokens for each number between 3-11 and one token for the 2 and 12, for a total of 18 tokens (the desert does not have a token).
Tokens also contain small dots (known as pips) that denote their likelihood of being rolled.
So, how do we normally create a board?
Well, the official Catan rulebook specifies two ways: either use the pre-generated layout, as specified in the booklet, or go for a random resource layout with a pre-determined token layout.
However, both methods clearly have downsides, as the pre-generated layout gets stale quickly and random layouts can easily be inbalanced.
For this reason, many people prefer using balanced board generators, such as this one and this one.
Fun fact: for the Catan championships, boards are pre-generated manually in advance, in order to ensure fairness.
Maybe they have their own tool?
You might be thinking that if generators already exist, then what's the point in developing a new one?
I feel like many of the generators are not extensive enough to guarantee proper balance.
At the same time, the ideal generator should also be configurable, allowing you to choose which balancing rules to enforce and which to relax.
It would also be cool if we can manually design a part of the board, and then have the generator do the rest.
For example, imagine that you want to play on a gimmicky board where all forests are next to each other, but don't really care about the rest of the layout.
That should be possible!
This then begs the question: what is balance? Which rules exist to create a balanced board?
After thinking and looking around on the internet, I put together the following list:
- The same resources should not touch
- Touching tiles cannot have the same token
- Probabilities should be balanced over a resource
- A tile intersection should not have more than 11 pips
How to hexagon?
As Catan boards are hexagonal, we should be able to express a hexagonal grid.
The thing is... how do we do that?
A square grid is simple: in a cartesian coordinate system, each cell is assigned an x and a y coordinate.
Neighbouring cells are those that are one x or y value apart from each other.
But how do we assign coordinates to a grid of hexes?
Turns out it's easy.
Red Blob Games has written an extensive guide, containing suggestions for multiple coordinate systems, their pros/cons, how to find a hex's neighbours, and more.
It's an incredibly interesting read, and I advise you to (at least briefly) read through it.
For the Catan board, we will be using axial coordinates.
Here, each hex is assigned a q and r coordinate.
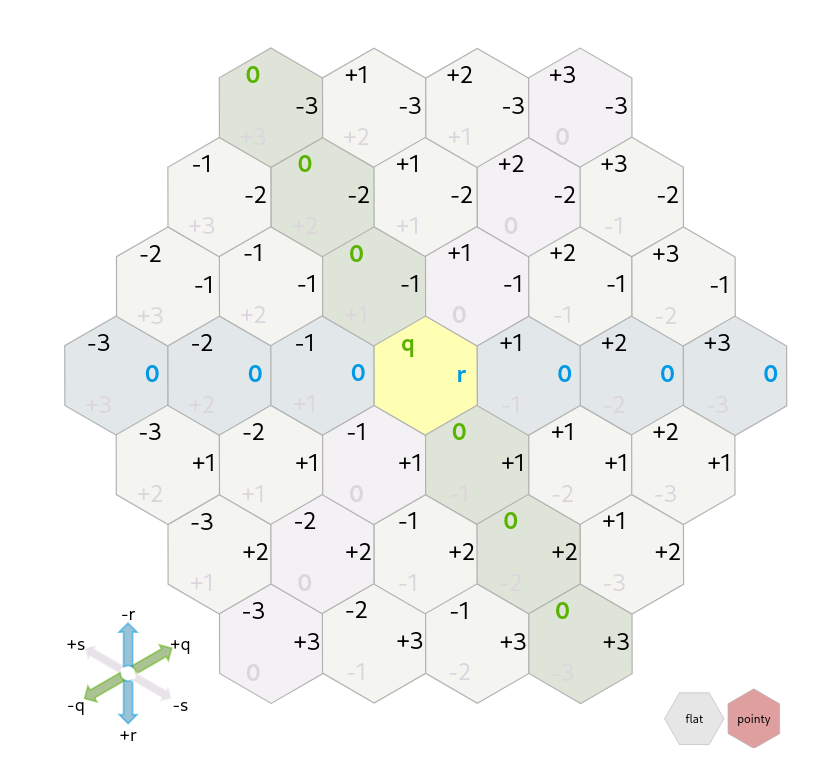Image taken from Red Blob Games
This system makes it easy to specify hexes via two coordinates.
It's also pretty straightforward to express what neighbours a specific hex has.
This is especially important as two of our proposed affect a tile's neighbours.
In the axial system, it suffices to do a simple addition/substraction to our tile's coordinates:
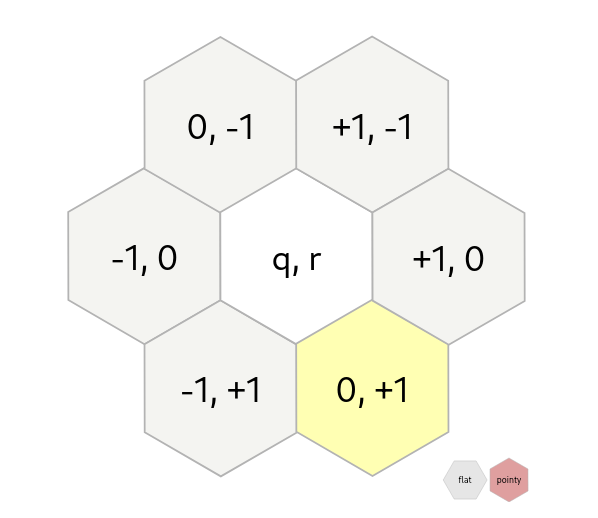Image taken from Red Blob Games
The IDP-Z3 reasoning engine
We can break down the problem of generating a balanced Catan board in a few steps:
- A board consists of 19 hexes
- Each hex requires a resource tile
- Each hex requires a token
- We want to impose some constraints on these tiles and tokens
One common way of tackling such problems is by using a reasoning engine such as the IDP-Z3 reasoning engine.
In IDP-Z3, we express knowledge in FO(·), an extension of First Order Logic, which is known to be quite readable.
Moreover, it is declarative: we do not have to program the solution to a problem, but rather the behavior of the problem.
In this case, we do not have to say how to generate a balanced board; we state what a correct board looks like, and let IDP-Z3 handle the rest.
Since our knowledge is general (and not operationalised), this also allows us re-use the knowledge to solve different subtasks.
Modeling Catan boards
Knowledge in IDP-Z3 is divided in three blocks: the vocabulary, the theory and the structure.
The vocabulary contains all the concepts over which we want to be able to reason.
Let's start simple, and just introduce the symbols necessary to assign a type and token to each hex of a board.
FO(·) is a typed logic: a type represents a domain of values, over which other symbols can express information.
First, we introduce our axial coordinates Q and R as types.
We specify their ranges as [-2..+2], as this suffices to model all 19 tiles.
Tile and token values are also types, which we introduce next.
Finally, we introduce two functions, which map their input arguments (e.g., Q and R) on an output argument (e.g., Tile or Token).
In this way, tile_type represents a tile for each hex coordinate.
vocabulary { type Q := {-2..2} type R := {-2..2} type Tile := {hills, forest, mountains, fields, pasture, desert, none} type Token := {1..12} tile_type : (Q ⨯ R) → Tile tile_token : (Q ⨯ R) → Token }
With this, we actually already have a Catan board generator!
Indeed, the IDP-Z3 system can use this information to start generating solutions:
tile_type := {(-2,-2)->desert, (-2,-1)->desert, (-2,0)->desert, (-2,1)->desert, (-2,2)->desert, (-1,-2)->fields, (-1,-1)->desert, (-1,0)->desert, (-1,1)->desert, (-1,2)->desert, (0,-2)->pasture, (0,-1)->fields, (0,0)->desert, (0,1)->desert, (0,2)->desert, (1,-2)->desert, (1,-1)->desert, (1,0)->desert, (1,1)->desert, (1,2)->desert, (2,-2)->desert, (2,-1)->desert, (2,0)->pasture, (2,1)->pasture, (2,2)->desert}. tile_token := {(-2,-2)->1, (-2,-1)->1, (-2,0)->1, (-2,1)->1, (-2,2)->1, (-1,-2)->1, (-1,-1)->1, (-1,0)->1, (-1,1)->1, (-1,2)->1, (0,-2)->1, (0,-1)->1, (0,0)->1, (0,1)->1, (0,2)->1, (1,-2)->1, (1,-1)->1, (1,0)->1, (1,1)->1, (1,2)->1, (2,-2)->1, (2,-1)->1, (2,0)->1, (2,1)->1, (2,2)->1}.
Oops!
While we have introduced the necessary symbols for a board, we haven't yet said what a correct board looks like!
Hence, it generated a board with mostly desert. That would be quite a tricky game of Catan!
IDP-Z3 allows us to express constraints in its theory block.
For instance, we might want to say that the desert must always be the desert tile.
tile_type(0, 0) = desert.
Now we have another problem: the tile_token function introduced earlier maps every set of coordinates on a token, including the coordinate of our desert.
But the desert normally doesn't have a token!
To overcome this, we simply state that the desert is always assigned 7 (and the 7 is always assigned the desert), no matter its coordinates.
∀q ∈ Q, r ∈ R: tile_token(q, r) = 7 ⇔ tile_type(q, r) = desert.
Here, we use quantification (∀) over the coordinates: for each coordinate pair (q, r) it must hold that if and only if the token assigned to that pair is a 7, it is also the desert.
While this may seem daunting at first, after a little practice this becomes incredibly intuitive to read.
We still have other issues: we can still have boards with more than one desert.
However, we can introduce a constraint that tells IDP-Z3 that we want exactly one desert tile.
In fact, we need to do the same for the other tile types!
For this, we use a count cardinality (#{...}), which will allow us to count the occurence of a resource.
This reads as "The number of (q, r) for which the tile type is desert should be equal to one".
We need to express a similar constraint on the tile tokens, but I have left it out for simplicity's sake.
#{q ∈ Q, r ∈ R: tile_type(q, r) = mountains} = 3.
Now we're getting somewhere: we can generate legal Catan boards!
tile_type := {(-2,-2)->fields, (-2,-1)->none, (-2,0)->pasture, (-2,1)->none, (-2,2)->mountains, (-1,-2)->fields, (-1,-1)->none, (-1,0)->fields, (-1,1)->forest, (-1,2)->pasture, (0,-2)->hills, (0,-1)->mountains, (0,0)->desert, (0,1)->none, (0,2)->none, (1,-2)->hills, (1,-1)->pasture, (1,0)->pasture, (1,1)->fields, (1,2)->none, (2,-2)->forest, (2,-1)->mountains, (2,0)->hills, (2,1)->forest, (2,2)->none}.
... or not? Why is tile (-2, -1) assigned none?
Well, it turns out we have too many coordinates: we need q and r to range between -2 and +2 to model our 19 hexes, but that actually models 25 hexes!
For instance, (-2, -2) is not a "real" hex as it is not part of our board.
Not to worry, we can solve this in a very IDP-Z3-like way by adding a predicate symbol relevant, which will denote what tiles are "real" and which are not.
This predicate is declared in the vocabulary as mapping on boolean:
relevant : (Q ⨯ R) → 𝔹
We can then use the structure block to enter the values of this new predicate.
In this case, we want it to contain all 19 coordinate pairs of our board.
structure { relevant := {(-2,0), (-2,1), (-2,2), (-1,-1), (-1,0), (-1,1), (-1,2), (0,-2), (0,-1), (0,0), (0,1), (0,2), (1,-2), (1,-1), (1,0), (1,1), (2,-2), (2,-1), (2,0)} }
This now allows us to state that each tile that is not relevant should be assigned tile value none and token value 1.
∀q ∈ Q, r ∈ R: ¬relevant(q, r) ⇔ tile_type(q, r) = none. ∀q ∈ Q, r ∈ R: ¬relevant(q, r) ⇔ tile_token(q, r) = 1.
And that's it! We can now succesfully generate correct Catan board layouts, using less than 30 lines of code.
That's already quite impressive, but we're not done yet!
Balancing our layouts
The whole point of developing this FO(·) specification was to use it for generating balanced Catan boards:
this is as simple as adding some constraints!
Take the "same resources should not touch" rule for example.
Here, we want to express a constraint over neighbouring hexes, so we first define what hexes are neighbours by adding a new predicate neighbour;
"neighbour: (Q ⨯ R ⨯ Q ⨯ R) → 𝔹".
In our theory, we want to then (a) express when tiles are neighbours, and (b) state that they may not share the same resource.
We can straightforwardly write these in FO(·) as follows:
∀q1, q2 ∈ Q, r1, r2 ∈ R: neighbour(q1, r1, q2, r2) ⇔ ¬(q1 = q2 ∧ r1 = r2) ∧ -1 ≤ (q1 - q2) ≤ 1 ∧ -1 ≤ (r1 - r2) ≤ 1 ∧ relevant(q1, r1) ∧ relevant(q2, r2). ∀q1, q2 ∈ Q, r1, r2 ∈ R: neighbour(q1, r1, q2, r2) ⇒ tile_type(q1, r1) ≠ tile_type(q2, r2).
In English, the first rule reads as "Two hexes neighbour if and only if they are not the same, their q and r coordinates are at most one apart and both hexes are relevant".
The second one reads "For each two hexes it must hold that if they neighbour, their tile type is different."
The next balancing change, "Probabilities should be balanced over a resource", aims to prevent that one resource is assigned too many low probability tokens, preventing a shortage from happening.
By low probability token, we mean any token that has 2 pips or less.
For example, for the resources that appear 4 times, a max of 2 may be assigned a token with a low pip count.
Of course, this requires that IDP-Z3 knows what pips are assigned to each token.
We introduce a new type
Pips, together with a function "token_pips: (Token) -> Pips" for which we assign the values in the structure.
This allows us to write a constraint as follows:
{q ∈ Q, r ∈ R: tile_type(q, r) = pasture ∧ token_pips(tile_token(q, r)) ≤ 2} < 3
Finally, we want to express that three neighbouring hexes may not share more than 11 pips between them, as those intersections would be too overpowered.
This is a bit more complex, but only because we need to quantify three times over the hexes.
If you take your time to interpret it, you will see that it's actually quite simple.
∀q1, q2, q3 ∈ Q, r1, r2, r3 ∈ R: neighbour(q1, r1, q2, r2) ∧ neighbour(q1, r1, q3, r3) ∧ neighbour(q2, r2, q3, r3) ⇒ token_pips(tile_token(q1, r1)) + token_pips(tile_token(q2, r2)) + token_pips(tile_token(q3, r3)) ≤ 11.
And there we have it!
We have used about 80 lines of FO(·) (including empty lines and comments) to express (a) what a correct Catan board looks like, and (b) what a balanced Catan board looks like.
Using this specification, we can generate our balanced boards!
If you feel inspired and want to play around with the specification yourself, you can open it in our online IDE.
Creating a web interface
Of course, while this works very well, it is a bit unwieldy to manually map the results on a real Catan board.
So, as a bonus, I have implented an interactive web interface!
Using IDP-Z3's API, it is actually quite trivial to embed the system in other applications.
In the interface, you can toggle on/off rules and generate boards.
But it is also interactive: you can set some tiles/tokens manually, and then have IDP-Z3 generate the rest according to the rules.
If you end up in a case where no board layout is feasible, the system will try to explain why no solution is possible.